
What is the Fibonacci Sequence – and why is it the secret to musical greatness?
Share
Geniuses from Mozart to Leonardo da Vinci have used the Fibonacci Sequence. But what is it and why does it make great music?
The Fibonacci Sequence has been nicknamed ‘nature’s code’, ‘the divine proportion’, ‘the golden ratio’, ‘Fibonacci’s Spiral’ amongst others.
What exactly is the Fibonacci Sequence?
Simply put, it’s a series of numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…
The next number in the sequence is found by adding up the two numbers before it. The ratio for this sequence is 1.618. This is what some people call ‘The Divine Proportion’ or ‘The Golden Ratio’.
When you make squares out of those values, it makes a nice-looking spiral:

Seem familiar? You've probably seen it before...

This sequence, pattern and spiral crop up in many things you might have never noticed. It is used in art and music; just look at how Leonardo da Vinci employed it in one of his most famous paintings, the Mona Lisa:

The Fibonacci Sequence in music
The Fibonacci Sequence plays a big part in Western harmony and musical scales. Here are the facts:
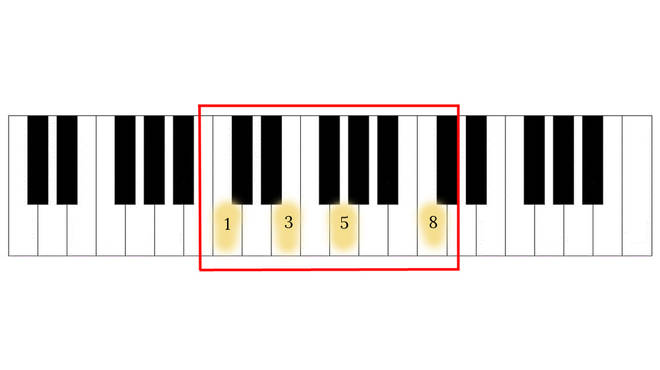
– An octave on the piano consists of 13 notes. Eight are white keys and five are black keys.
– A scale is composed of eight notes, of which the third and fifth notes create the foundation of a basic chord
– In a scale, the dominant note is the fifth note, which is also the eighth note of all 13 notes that make up the octave.
– Eight divided by 13 equals 0.61538... the approximate Golden Ratio)
Starting to see a pattern? These are all numbers in the Fibonacci Sequence: 3, 5, 8, 13.
Who used the Fibonacci Sequence?
Composers and instrument makers have been using the Fibonacci Sequence and the Golden Ratio for hundreds of years to compose and create music.
Mozart, for instance, based many of his works on the Golden Ratio – especially his piano sonatas.
The traditional sonata has two parts:
1. Exposition – where the musical theme is introduced
2. Development and recapitulation – where the theme is developed and repeated
Now, here's the interesting bit...
Mozart arranged his piano sonatas so that the number of bars in the development and recapitulation divided by the number of bars in the exposition would equal approximately 1.618, the Golden Ratio.
Let's take the first movement of Mozart's Piano Sonata No. 1 in C Major as an example.
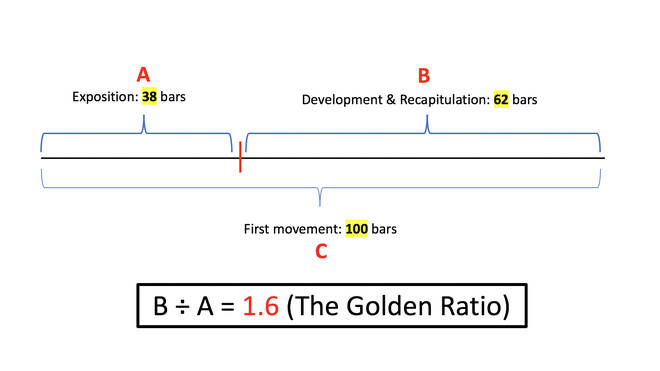
In the above diagram, C is the sonata's first movement as a whole, B is the development and recapitulation, and A is the exposition.
The exposition consists of 38 bars and the development and recapitulation consists of 62. The first movement as a whole consists of 100 bars.
62 divided by 38 equals 1.63 (approximately the Golden Ratio)
Experts claim that Beethoven, Bartók, Debussy, Schubert, Bach and Satie (to name a few) also used this technique to write their sonatas, but no one is exactly sure why it works so well.
Stradivari
Hailed as the master of violin making, Antonio Stradivari has made some of the most beautiful and sonorous violins in existence.
To save the sound of a Stradivarius, this entire Italian city is keeping quiet
There's a reason a Stradivarius violin would cost you a few million pounds to buy – and its value is partly down to the Fibonacci Sequence and its Golden Ratio.
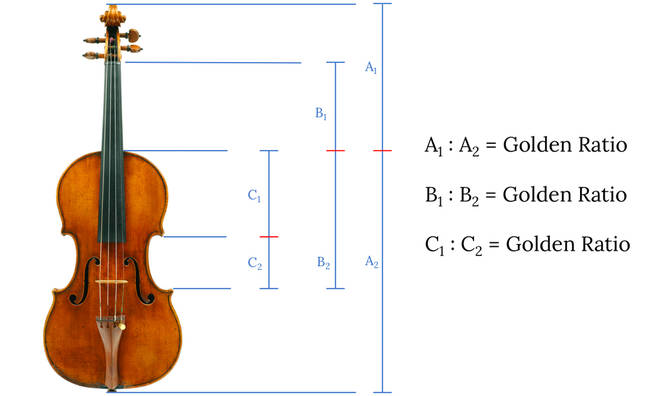
The Golden Ratio can be found throughout the violin by dividing lengths of specific parts of the violin. Some people think this is one of the reasons it sounds so good.
As well as being used to craft violins, the Golden Ratio that comes from the Fibonacci Sequence is also used for saxophone mouthpieces, in speaker wires, and even in the acoustic design of some cathedrals.
Even Lady Gaga has used it in her music – find out how here >
